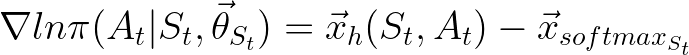Jack O'Grady

Overview

After trying to solve this problem unsuccessfully with an episodic Q-learning agent, I completely redesigned the agent based on new knowledge I acquired about reinforcement learning, problem construction, and agent design.

When discussing issues with the Q-learning agent, we had four questions:

• How can we explore more intelligently?

  • Using a softmax policy, we can explore actions and states considering their relative expected value as opposed to randomly selecting from any of the non-max values in the epsilon greedy policy

• How do we decouple action selection from action values?

  • Using an actor-critic design, the actor learns action selection probabilities while the critic learns action/state values and helps shape the actor’s selections during the update

• How should we adapt to the continuous nature of this problem?

  • We can use a value update function that calculates error based on average reward without a discount factor (only used for episodic tasks, which this is not)

• How can we arrive at the optimal state earlier?

  • My hypothesis is that these targeted changes and agent redesign will allow the agent to find the max state earlier and have less variance in its exploration

Softmax Actor-Critic

Before we discuss the overall agent design, reward function, and agent update process, let’s quickly review the actor-critic algorithm. At a high level, the actor learns the policy and selects actions, while the critic learns an estimate of state or action values. The critic calculates error, which updates the probability of selecting certain actions in the actor and updates the value estimates inside of the critic. The critic is uninvolved in action selection, and the actor is uninvolved in value updates.

Agent Design

Interaction with System

To interface with the solar panel, the agent will select an action (or state, since they are one in the same here). The agent utilizes a flat-map index, but any communication with the actual solar panel entails converting back and forth from the flat-map index to a 2D index of motor position. After each action selection, the agent also receives a measure of power from the solar panel which is captured in the reward function.

State & Action Representation in Agent

Both the actor and the critic will use a table to represent their values as the state-space is small enough. Future additions to do this will demonstrate the performance using function approximation via a neural network to hold values (this generalizes better to other problems). A reminder that the critic’s table holds state value estimates, whereas the actor’s table holds probabilities of selecting a given action in a given state.

Action Selection

During action selection, the vector of all actions for a given state will generate a softmax vector from which an index will be selected according the softmax-calculated distribution. The chosen action will be a single index, which is then converted from flat-map to motor positions for interacting with the environment.

Reward Function

In the initial agent, I was using power received as the only factor of the reward function. This omits a key factor of the agent’s decisions: the power consumed by the motors to transition to different states.

• The motors use more power to go to states that are farther away (more degrees of rotation away). So, getting to index [36, 36] from [0,0] requires more energy than from [30, 18]

• Exploring more states is “costlier” to the agent, so giving the agent a feedback mechanism for motor power consumption will let it figure out how to balance exploration with maximizing energy over time

The below equation shows the reward function that the agent will use:

Here, motor draw is defined as some constant sigma (which captures the power draw per degree moved) multiplied by the total number of degrees moved (the sum of motor 1 and motor 2’s movements). Rather than using the actual 0-180° positions, we’ll use the 2D motor index positions from 0-36.

Agent Learning

The below diagram illustrates an overview of the learning process for the actor-critic agent. First, we calculate error. After that, we use the calculated error to update the actor and critic independently of each other. With the updates made, we repeat the action selection and interaction with environment, then update again.

Error Calculation

Starting with error, we calculate it based on the difference between the reward we received and the average reward (R bar) that the agent has been receiving. Additionally, to make the updates smoother, we add a baseline from the critic in which we also compute the difference between what the critic values the state we just transitioned to as compared to the critic’s value of the state we were in before.

To visualize how the critic calculates state value, it essentially sums all the q-values for all the actions in a given state to get an overall state value. Essentially, it’s saying “Is the entirety of the possibilities of the state we just entered better than or worse than the state we just came from?”

After we calculate error, we need to update our value for average reward. The average reward, actor, and critic all have their own step-size parameters alpha. Below is the equation for updating the average reward value.

Critic Update

Next, we update the critic by simply adding the error times step size to the previous action-value estimated by the critic for a given state, action pair.

Actor Update

Separate from the critic, we need to update the actor’s policy. Actor-Critic algorithms are part of a larger family or RL algorithms known as policy-gradient methods. In each of these, we are directly editing the agent’s policy, which is captured as theta. Think of the theta vector as a 1D vector containing probabilities for each action in a given state. If the agent got more reward than it thought, we’ll amplify the probability of selecting the action that was just taken and reduce the probability of the other actions proportional to the error multiplied by a step size. If the opposite occurs, we’ll reduce the probability of the action taken and increase the probability of the other actions.

Generally speaking, the policy update equation is below, where the delta ln term is the gradient. Since we’re in the vector space, the gradient term is essentially capturing what direction each individual index of the vector should be updated with, and by how much.

Breaking down the gradient term, for a softmax agent this becomes:

Let’s understand what the above equation is saying. Here, x is a one-hot encoded vector of the action index that was chosen at time t. So, if we had four actions and action three was chosen, x would look like [0 0 1 0]. The second part of the equation is taking the sum of [the probability of selecting action b in state S with theta policy multiplied by the one-hot encoded vector for that action in this state]. For any action b, this essentially produces a vector with the only value being the softmax probability of action b being taken. Let’s say action 1 was taken and it had probability of 0.33 of being selected. The term would be [0.33 0 0 0].

Now, since we have to sum all of these and each will only ever have one term that the other’s have a 0 in, we’ll end up with a vector of the softmax probabilities or each action.

Alas, we return to our original equation for updating the policy vector with a simplified equation that we can actually implement in code as we have values for all of the terms.

The performance of this agent will be discussed on a future experiment result page which will be linked below!

< Back to Index