The Problem Statement
This page introduces the problem we’re attempting to solve with a reinforcement learning agent, as well as broadly the types of problems that RL is well-suited to solve.
Introduction
In 2020, I started teaching myself about Artificial Intelligence (AI) primarily in the context of neural networks and deep learning. While this was immensely cool to learn about, it didn’t solve a lot of the key issues and questions I’d had after working on complex electrochemical systems in the renewables space over the prior 3-ish years.
At the highest level, I think AI can be classified into two separate domains:
prediction/estimation/classification problems
control problems
The first lets us estimate values for things that are traditionally very hard or too computationally expensive to model. While the prediction of some value is useful, it’s only half of the equation. We usually want to do something based on that information, and the new quantity we predicted or estimated may be a key enabler in enabling us to perform better, but the value alone doesn’t tell us how to perform something. Furthermore, when there are many, many values of a complex system that influence how it should be optimally controlled, it becomes harder and harder for humans (or traditional control methods) to try and solve.
This is where the second facet of AI comes in: problems of optimal control. Reinforcement learning solves this class of problems. Now, before we go into any more detail on what reinforcement learning is, let’s define a tangible problem that we’ll use as our learning sandbox.
Energy Optimization Problem
Back in 2018, I interned at a utility-scale solar developer. As I thought more and more about solar with my background in Physics, there was one thought experiment that always seemed to stump me:
On a completely cloudy day, what would be the optimal way to position a solar panel?
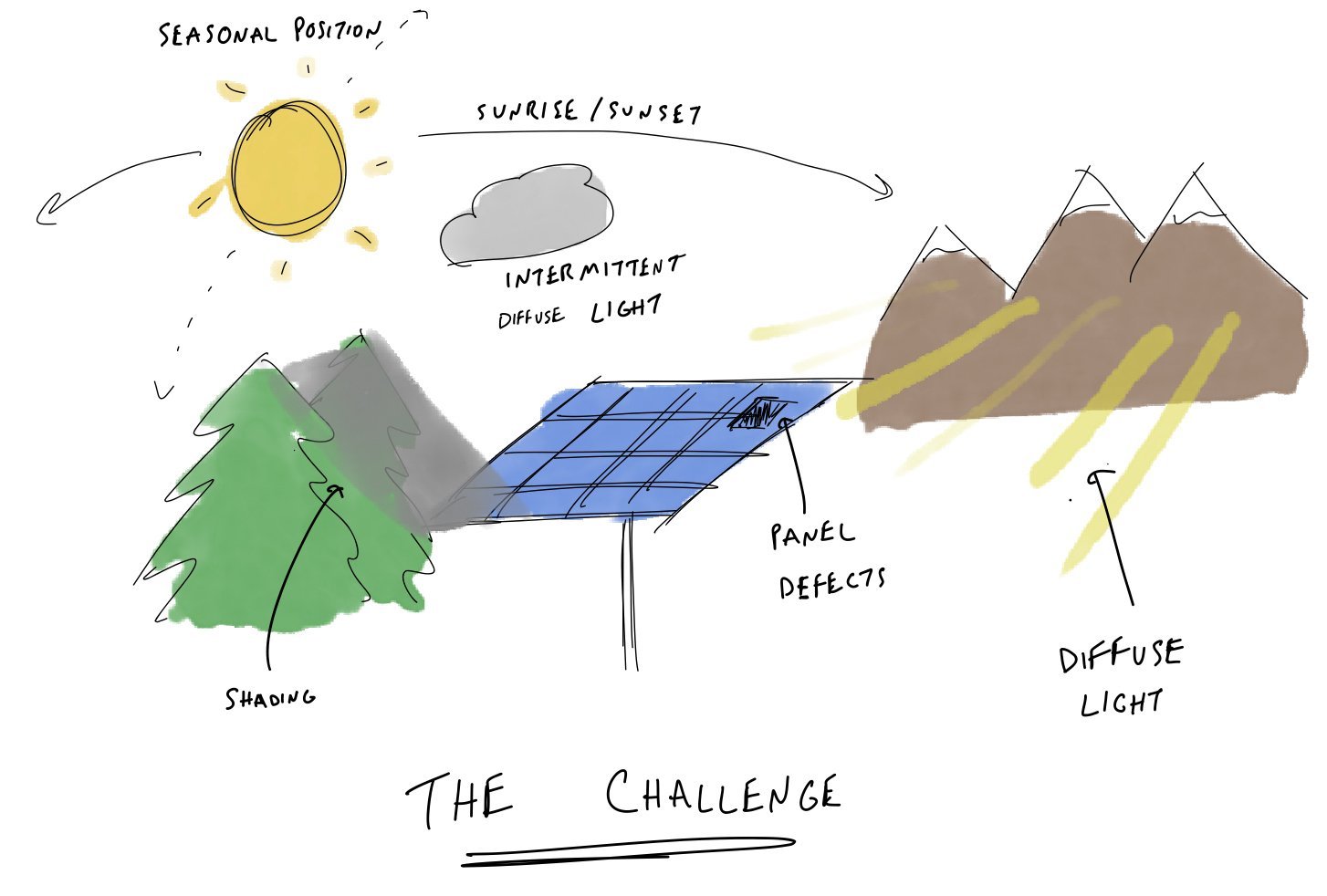
Modeling a solar asset without clouds, shading, panel defects, etc. is a fairly straightforward task: we know the position of the sun at every time of day for every place on Earth. Yet, when we introduce clouds, it’s nearly impossible to model for. There’s no way to know exactly how clouds will diffuse light, and no two clouds are the same.
In this case, clouds are just one example of added complexity to the solar modeling problem. Enumerating a few more of them:
Nearby structures (in this case trees) can shade the panel at various positions throughout the day
Other nearby structures can add diffuse light from reflection which cannot be easily modeled
Lastly, the panel itself may have local defects which affect the nominal energy output in certain positions
Problem Complexities: In this figure, we see all the different factors at play which affect the optimal position of the solar panel
Without these factors, the environment that the solar panel is in is essentially deterministic. Yet, with these factors, the environment can become highly stochastic. Furthermore, the environment is constantly changing, making it non-stationary. In the real world, we’d really just think about the position of the sun as it’s the first order effect driving energy production and try to ensure that our panels aren’t shaded by any nearby structure. I always wondered how we could go beyond this, though, and try to account for all of these other factors.
Let’s say that our objective is to maximize the energy output of a solar panel, and our solar panel has a dual-axis system for positioning itself.
Thinking of the factors we just discussed in three broad categories, let’s elaborate on the effects of each:
Ambient factors
Panel-Induced factors
Control-Induced factors
Ambient Factors
In this optimization problem, the ambient conditions are continuously changing:
The sun changes position in the sky as both a function of the time of day and the season. Thus, the panel will need to continuously change position throughout the day (in different ways as the season changes) to optimize energy production.
The sun may be blocked by clouds, which creates a myriad of potential diffuse lighting scenarios.
The sun may reflect off of nearby objects differently at different times of the day, and the reflection may not be considered in a traditional plant model for optimizing panel positions.
External structures or plants may shade certain parts of the panel, causing unaccounted-for energy losses. Even when accounted for, these structures may change over time, either necessitating maintenance (to remediate the structure’s interference) or an updated plant model.
Panel-Induced Factors
In addition to the dynamic environment the panel operates in, the panel itself adds complexity to the problem:
Certain cells or modules in the photovoltaic panel may malfunction and stop producing energy. This may warrant a new panel arrangement to optimize the remaining functioning cells that is not accounted for in the plant model.
Upstream electronics from the solar panel may be functioning sub-optimally, thereby causing a reduction in net energy when the panel itself is positioned optimally.
Control-Induced Factors
Lastly, even when accounting for ambient and panel-induced factors, what we do with that information can lead to other optimization considerations.
The incremental energy-consumption to adjust a panel’s position may outweigh the incremental energy increase of the new position. The “cost” of updating the position of the solar panel must be considered as it affects the net energy output of the system.
Solving the Problem without RL
Considering that the sun’s position in the sky is probably the leading order of magnitude contribution to solar energy output, a classical model would probably contain the following logic:
panel-angle lookup table based on time of day, day of year
pre-programmed deterministic logic (if any) to attempt to handle diffuse lighting scenarios (cloudy days)
timed updates of panel position to account for the energy loss from moving panels
human monitoring and maintenance of shading interference
This certainly would create a well-functioning solar array, but is it truly optimal? What happens if…
the diffuse lighting logic is not actually optimal?
parts of the panel degrade such that the panel-angle lookup table is no longer optimal?
the panel-angle lookup table is not optimal for the specific location of the panel?
there could actually be more net energy produced with more frequent updates to the position of the panels based on time of day?
all of the above combine at the same time, creating unique combinations of the effects discussed above?
This suddenly becomes a massive, massive state-space to have to model. The state-space is also non-stationary, meaning that behavior observed on one day or in one condition may not be the same behavior observed in those same conditions over time (panels degrade, surroundings change, etc).
Solving the Problem with RL
Reinforcement learning is a paradigm shift for solving complex optimization problems because:
We do not need to have a detailed model of the underlying system to achieve optimal behavior
We can simply work backwards from the reward for our system (in this case net energy produced) and let the RL agent determine the optimal behavior on its own (called a policy)
The RL agent can continuously learn from its actions to update the choices it makes, resolving the non-stationary induced complexities
Thus, RL is very well-suited to tackle our solar energy optimization problem. Yet, for those unfamiliar with RL, what even is it? Head to the page below to learn about some key concepts of RL: